What is the shape of the Universe? If you had come along before the 1800s, it likely never would have occurred to you that the Universe itself could even have a shape. Like everyone else, you would have learned geometry starting from the rules of Euclid, where space is nothing more than a three-dimensional grid. Then you would have applied Newton’s laws of physics and presumed that things like forces between any two objects would act along the one and only straight line connecting that. But we’ve come a long way in our understanding since then, and not only can space itself be curved by the presence of matter and energy, but we can witness those effects.
It didn’t have to be the case that the Universe, as a whole, would have a spatial curvature to it that’s indistinguishable from flat. But that does seem to be the Universe we live in, despite the fact that our intuition might prefer it to be shaped like a higher-dimensional sphere. The model of the Universe as:
- originating from a point,
- expanding outwards in all directions equally,
- reaching a maximum size and being drawn back together by gravity,
- and eventually recollapsing down into a Big Crunch,
was one that was preferred by many theoretical physicists throughout the 20th century. But there’s a reason we go out and measure the Universe instead of sticking to our theoretical prejudices: because science is always experimental and observational, and we have no right to tell the Universe how it ought to be.
And while “flat” might be the Universe we get, it isn’t some “three-dimensional grid” like you might typically intuit. Here’s what a flat Universe is, as well as what it isn’t.

In Euclidean geometry, which is the geometry that most of us learn, there are five postulates that allow us to derive everything we know of from them.
- Any two points can be connected by a straight line segment.
- Any line segment can be extended infinitely far in a straight line.
- Any straight line segment can be used to construct a circle, where one end of the line segment is the center and the other end sweeps radially around.
- All right angles are equal to one another, and contain 90° (or π/2 radians).
- And that any two lines that are parallel to each other will always remain equidistant and never intersect.
Everything you’ve ever drawn on a piece of graph paper obeys these rules, and the thought was that our Universe just obeys a three-dimensional version of the Euclidean geometry we’re all familiar with.
But this isn’t necessarily so, and it’s the fifth postulate’s fault. To understand why, just look at the lines of longitude on a globe.
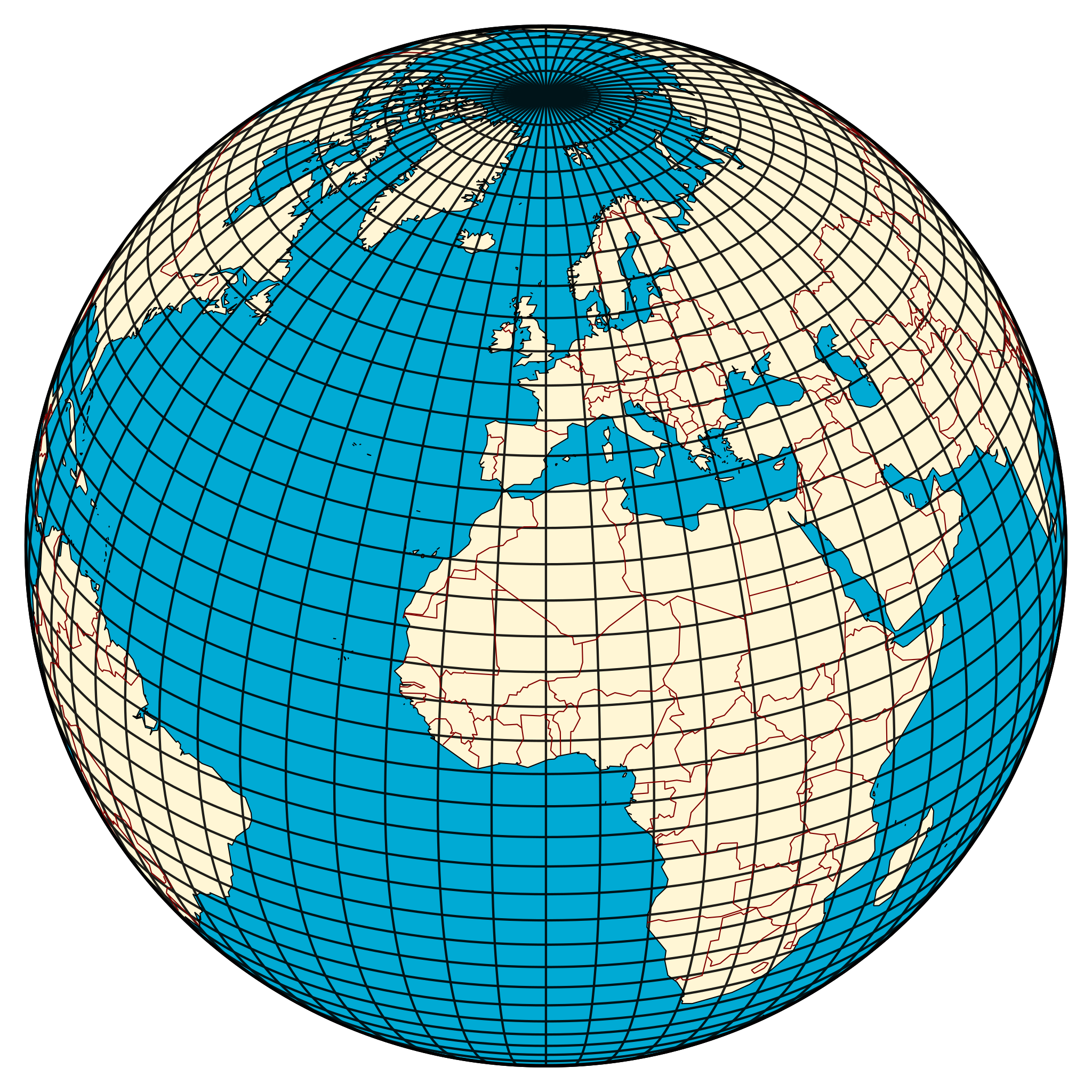
Every line of longitude you can draw makes a complete circle around the Earth, crossing the equator and making a 90° angle wherever it does. Since the equator is a straight line, and all the lines of longitude are straight lines, this tells us that — at least at the equator — the lines of longitude are parallel. If Euclid’s fifth postulate were true, then any two lines of longitude could never intersect.
But lines of longitude do intersect. In fact, every line of longitude intersects at two points: the north and south poles.
The reason is the same reason that you can’t “peel” a sphere and lay it out flat to make a square: the surface of a sphere is fundamentally curved and not flat. In fact, there are three types of fundamentally different spatial surfaces. There are surfaces of positive curvature, like a sphere; there are surfaces of negative curvature, like a horse’s saddle; there are surfaces of zero curvature, like a flat sheet of paper. If you want to know what the curvature of your surface is, all you have to do is draw a triangle on it — the curvature will be easier to measure the larger your triangle is — and then measure the three angles of that triangle and add them together.
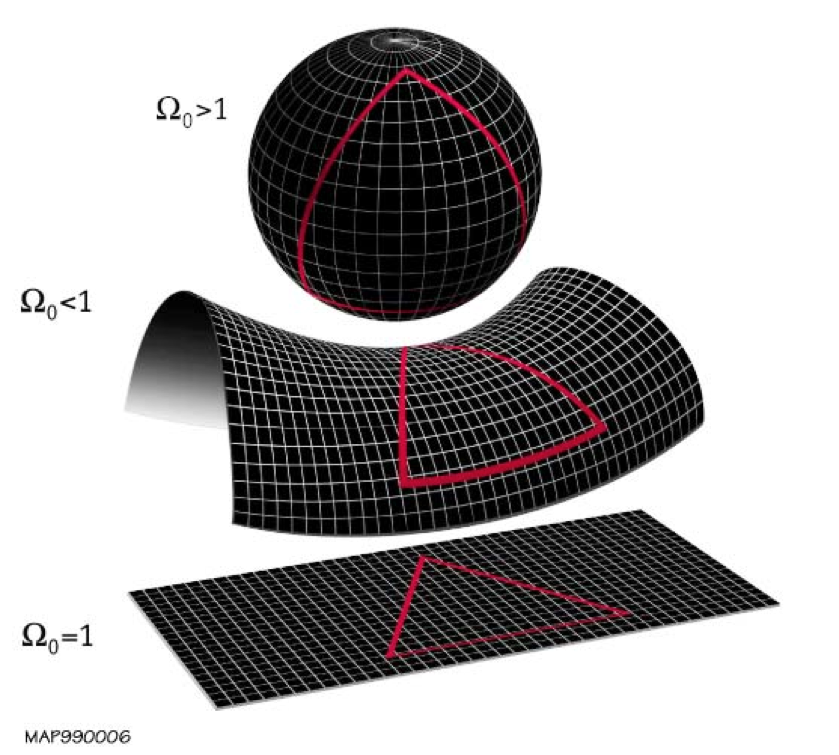
Most of us are familiar with what happens if we draw a triangle on a flat, uncurved sheet of paper: the three interior angles of that triangle will always add up to 180°. But if you instead have a surface of positive curvature, like a sphere, your angles will add up to a greater number than 180°, with larger triangles (compared to the sphere’s radius) exceeding that 180° number by greater amounts. And similarly, if you had a surface of negative curvature, like a saddle or a hyperboloid, the interior angles will always add up to less than 180°, with larger triangles falling farther and farther short of the mark.
This realization — that you can have a fundamentally curved surface that doesn’t obey Euclid’s fifth postulate, where parallel lines can either intersect or diverge — led to the now-almost 200 year old field of non-Euclidean geometry. Mathematically, self-consistent non-Euclidean geometries were demonstrated to exist independently, in 1823, by Nicolai Lobachevsky and Janos Bolyai. They were further developed by Bernhard Riemman, who extended these geometries to an arbitrary number of dimensions and wrote down what we know of as a “metric tensor” today, where the various parameters described how any particular geometry was curved.
In the early 20th century, Albert Einstein used Riemann’s metric tensor to develop General Relativity: a four-dimensional theory of spacetime and gravitation.
In straightforward terms, Einstein realized that thinking of space and time in absolute terms — where they didn’t change under any circumstances — didn’t make any sense. In special relativity, if you traveled at speeds close to the speed of light, space would contract along your direction of motion, and time would dilate, with clocks running slower for two observers moving at different relative speeds. There are rules for how space and time transform in an observer-dependent fashion, and that was just in special relativity: for a Universe where gravitation didn’t exist.
But our Universe does have gravity. In particular, the presence of not only mass, but all forms of energy, will cause the fabric of spacetime to curve in a particular fashion. It took Einstein a full decade, from 1905 (when special relativity was published) until 1915 (when General Relativity, which includes gravity, was put forth in its final, correct form), to figure out how to incorporate gravity into relativity, relying largely on Riemann’s earlier work. The result, our theory of General Relativity, has passed every experimental test to date.
What’s remarkable about it is this: when we apply the field equations of General Relativity to our Universe — our matter-and-energy filled, expanding, isotropic (the same average density in all directions) and homogeneous (the same average density in all location) Universe — we find that there’s an intricate relationship between three things:
- the total amount of all types of matter-and-energy in the Universe, combined,
- the rate at which the Universe is expanding overall, on the largest cosmic scales,
- and the curvature of the (observable) Universe.

The Universe, in the earliest moments of the hot Big Bang, was extremely hot, extremely dense, and also expanding extremely rapidly. Because, in General Relativity, the way the fabric of spacetime itself evolves is so thoroughly dependent on the matter and energy within it, there are really only three possibilities for how a Universe like this can evolve over time.
- If the expansion rate is too low for the amount of matter-and-energy within your Universe, the combined gravitational effects of the matter-and-energy will slow the expansion rate, cause it to come to a standstill, and then cause it to reverse directions, leading to a contraction. In short order, the Universe will recollapse in a Big Crunch.
- If the expansion rate is too high for the amount of matter-and-energy within your Universe, gravitation won’t be able to stop and reverse the expansion, and it might not even be able to slow it down substantially. The danger of the Universe experiencing runaway expansion is very great, frequently rendering the formation of galaxies, stars, or even atoms impossible.
- But if they balance just right — the expansion rate and the total matter-and-energy density — you can wind up with a Universe that both expands forever and forms lots of rich, complex structure.
This last option describes our Universe, where everything is well-balanced, but it requires a total matter-and-energy density that matches the expansion rate exquisitely from very early times.
The fact that our Universe exists with the properties we observe tells us that, very early on, the Universe had to be at least very close to flat. A Universe with too much matter-and-energy for its expansion rate will have positive curvature, while one with too little will have negative curvature. Only the perfectly balanced case will be flat.
But it is possible that the Universe could be curved on extremely large scales: perhaps even larger than the part of the Universe we can observe. You might think about drawing a triangle between our own location and two distant galaxies, adding up the interior angles, but the only way we could do that would involve traveling to those distant galaxies, which we cannot yet do. We’re presently limited, technologically, to our own tiny corner of the Universe. Just like you can’t really get a good measurement of the curvature of the Earth by confining yourself to your own backyard, we can’t make a big enough triangle when we’re restricted to our own Solar System.
Thankfully, there are two major observational tests we can perform that do reveal the curvature of the Universe, and both of them point to the same conclusion.
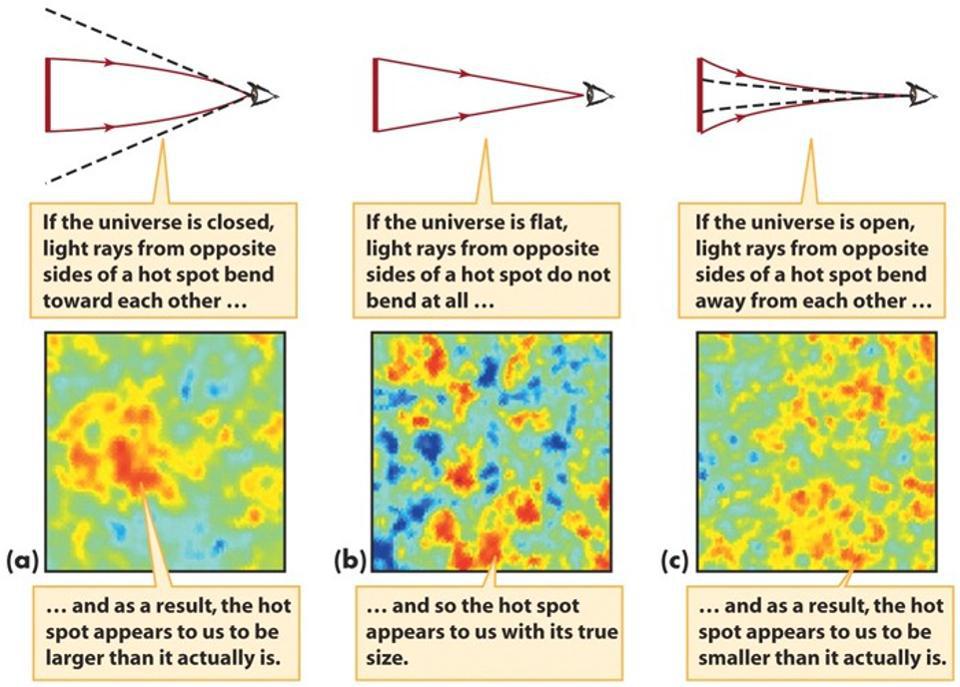
1.) The angular size of the temperature fluctuations that appear in the Cosmic Microwave Background. Our Universe was very uniform in the early stages of the hot Big Bang, but not perfectly uniform. There were tiny imperfections: regions that were slightly more or less dense than average. There’s a combination of effects that take place between gravity, which works to preferentially attract matter and energy to the denser regions, and radiation, which pushes back against the matter. As a result, we wind up with a set of patterns of temperature fluctuations that get imprinted into the radiation that’s observable, left over from the hot Big Bang: the cosmic microwave background.
These fluctuations have a particular spectrum: hotter or colder by a certain amount on specific distance scales. In a flat Universe, those scales appear as they are, while in a curved Universe, those scales would appear larger (in a positively curved Universe) or smaller (in a negatively curved Universe). Based on the apparent sizes of the fluctuations we see, from the Planck satellite as well as other sources, we can determine that the Universe is not only flat, but it’s flat to at least a 99.6% precision.
This tells us that if the Universe is curved, the scale on which its curved is at least ~250 times larger than the part of the Universe that’s observable to us, which is already ~92 billion light-years in diameter.
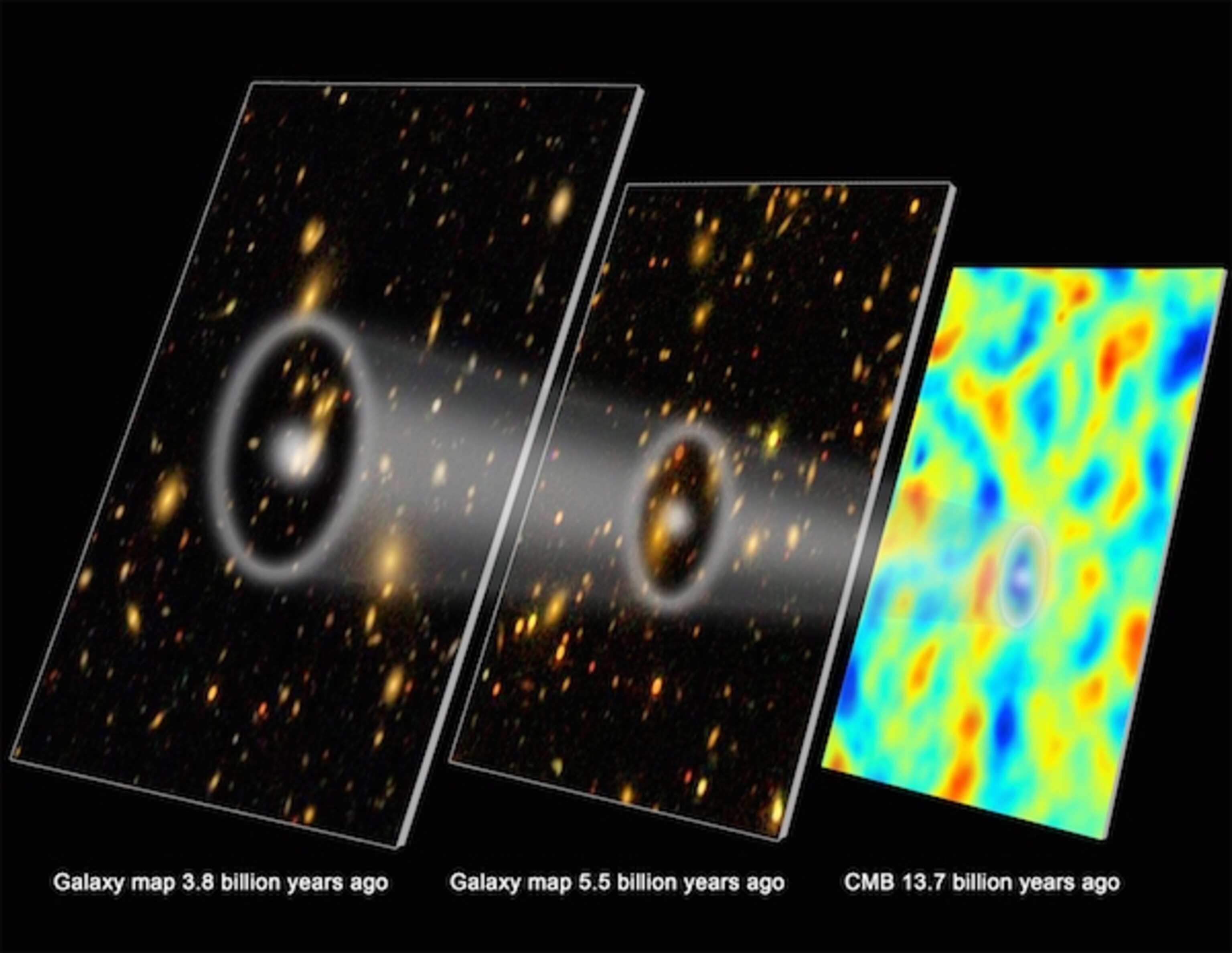
2.) The apparent angular separations between galaxies that cluster at different epochs throughout the Universe. Similarly, there’s a specific distance scale that galaxies are more likely to cluster along. If you put your finger down on any one galaxy in the Universe today, and moved a certain distance away, you can ask the question, “How likely am I to find another galaxy at this distance?” You’d find that you would be most likely to find one very nearby, and that distance would decrease in a particular way as you moved away, with one exceptional enhancement: you’d be slightly more likely to find a galaxy about 500 million light-years away than either 400 or 600 million light-years away.
That distance scale has expanded as the Universe has expanded, so that “enhancement” distance is smaller in the early Universe. However, there would be an additional effect superimposed atop it if the Universe were positively or negatively curved, as that would affect the apparent angular scale of this clustering. The fact that we see a null result, particularly if we combine it with the cosmic microwave background results, gives us an even more stringent constraint: the Universe is flat to within ~99.75% precision.
In other words, if the Universe isn’t curved — for example, if it’s really a hypersphere (the four-dimensional analogue of a three-dimensional sphere) — that hypersphere has a radius that’s at least ~400 times larger than our observable Universe.
All of that tells us how we know the Universe is flat. But to understand why it’s flat, we have to look to the theory of our cosmic origins that set up the Big Bang: cosmic inflation. Inflation took the Universe, however it may have been previously, and stretched it to enormous scales. By the time that inflation ended, it was much, much larger: so large that whatever part of it remains is indistinguishable from flat on the scales we can observe it.
The only exception to the flatness is caused by the sum of all the quantum fluctuations that can get stretched across the cosmos during inflation itself. Based on our understanding of how these fluctuations work, it leads to a novel prediction that has yet to be tested to sufficient precision: our observable Universe should actually depart from perfect flatness at a level that’s between 1-part-in-10,000 and 1-part-in-1,000,000.
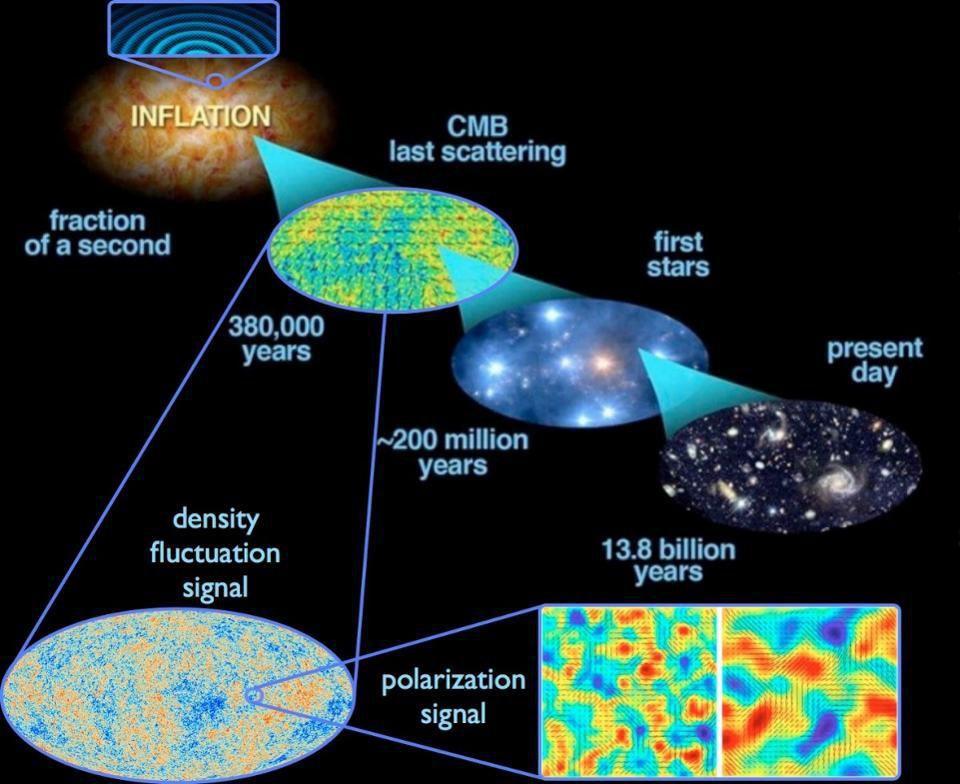
Right now, we’ve only measured the curvature to a level of 1-part-in-400, and find that it’s indistinguishable from flat. But if we could get down to these ultra-sensitive precisions, we would have the opportunity to confirm or refute the predictions of leading theory of our cosmic origins as never before. We cannot know what its true shape is, but we can both measure and predict its curvature.
This is one of the major goals of a series of upcoming missions and observational goals, with the new generation of Cosmic Microwave Background measurements poised to measure the spatial curvature down to 1-part-in-1000 or better, and with the Roman Telescope, the EUCLID mission, and Rubin Observatory all planned to come online and measure the baryon acoustic oscillation signature better and more precisely than ever before.
Although the Universe appears indistinguishable from flat today, it may yet turn out to have a tiny but meaningful amount of non-zero curvature. A generation or two from now, depending on our scientific progress, we might finally know by exactly how much our Universe isn’t perfectly flat, after all, and that might tell us more about our cosmic origins, and what flavor of inflation actually occurred, than anything else ever has.
This article was reprinted with permission of Big Think, where it was originally published.





