If you were to look at the Universe on the absolute largest of cosmic scales, you’d find that galaxies cluster together in an enormous web of structure. Individual galaxies form along the threads of the web, with rich groups and clusters of galaxies forming at the nexuses where the threads meet. In between those threads are giant void regions, with far fewer galaxies than average, and some voids that are so deep they seem to harbor no galaxies at all. This web, to the best of our knowledge, is dominated by dark matter’s gravitational effects, but it’s only the normal matter — made of protons, neutrons, and electrons — that winds up forming the stars, gas, and dust that we can observe.
However, there ought to be an extra structural effect that isn’t so easy to see: a clustering feature known as baryon acoustic oscillations. Dating back to the very early stages of cosmic history and caused by normal matter getting “bounced” away from a clustering center, it leaves an imprint that looks a bit like a cosmic bubble: where galaxies are more likely to be found a specific distance away from another rather than slightly closer or farther away. Although this feature has been seen statistically before, no individual “bounce” or “bubble” has ever been seen before.
In a brand new paper, astronomers Brent Tully, Cullan Howlett, and Daniel Pomarède present evidence for the very first individual baryon acoustic oscillation ever discovered in the entire Universe. Here’s the science behind it.

The simplest way to make a prediction for what you expect to be there in the Universe is to simultaneously know two things.
- First, you must know the initial conditions of your physical system: what’s in your system, where it all is, and what its properties are.
- And second, you must know the laws and rules that govern your system and its time-evolution.
This is the principle behind making predictions for any physical system you can possibly consider, from something as simple as a falling mass governed by Newton’s F = ma to something as complex as the entire observable Universe.
So if we want to answer the question of what “types of structure we expect will exist in the Universe,” all we have to do is specify those two things. The first is straightforward: we need to know the initial conditions that the Universe was born with, including its ingredients, properties, and distribution. And the second, in principle, is also straightforward: to then use the equations that describe the governing laws of physics to evolve your system forward in time, all the way until you reach the present day. It may sound like a daunting task, but science is up to the challenge.

The Universe, at the start of the hot Big Bang, was born filled with matter, antimatter, radiation, and was almost — but not quite — perfectly uniform in nature. This tiny bit of nonuniformity, the cosmological inhomogeneities, are simply imperfections in how uniformly dense the Universe is at the very beginning.
- They appear equally on all scales: small, medium, and large cosmic scales alike.
- They follow what we call a “normal” distribution, where the strength of the nonuniformity follows a Bell curve: half greater-than-average and half less-than-average, with 68% within 1 standard deviation of the mean, 95% within 2 standard deviations of the mean, 99.7% within 3 standard deviations of the mean, etc.
- They have an amplitude of about 1-part-in-30,000, meaning that 32% of all regions are at least 1-part-in-30,000 away from the average value (half above and half below), 5% are at least 2-parts-in-30,000 away from average, 0.3% are at least 3-parts-in-30,000 away from average, etc.
- And the imperfections that exist on all these different scales are superimposed atop one another, with medium-scale imperfections atop large-scale imperfections and with smaller-scale imperfections atop all of those.
Physically, we characterize this as a nearly perfectly scale-invariant spectrum, and it tells us what the density was like in the Universe right at the start of the hot Big Bang.

But then the Universe evolves: it expands, cools, and gravitates. Unstable particles decay into lighter, more stable ones. Matter and antimatter annihilate away, leaving only a tiny bit of excess matter amidst a sea of radiation: photons and neutrinos and antineutrinos. Dark matter is present as well, with five times the overall abundance as normal matter. After a few minutes, protons and neutrons start fusing together, creating the light atomic nuclei: formed before any stars ever could. But it will take a whopping 380,000 years, on average, before the Universe cools enough to allow neutral atoms to form.
This is the key time over which we need to understand how the seeds of cosmic structure evolve. If you take a very broad view of things, you’ll say, “It just gravitates, and even though radiation pushes back against structures that try to gravitationally collapse, those structures will still slowly and gradually grow, even as radiation streams out of them.” This is true, and is known as the Mészáros effect: the way by which early seeds of structure gravitationally grow in the early, post-Big Bang Universe.
But there’s more to the story, and we’ll see it if we look at the Universe in just a little more detail.

Instead of saying there’s “matter and radiation in the Universe,” let’s now go a step further and say there’s “normal matter, made of electrons and nuclei, plus dark matter, plus radiation.” In other words, we now have three components in our Universe: normal matter, dark matter, and radiation, rather than just lumping the normal and dark matter together in the category of “matter.” Now, something slightly different occurs.
When you have an overdense region, all of the matter and energy gets gravitationally attracted toward it, and it begins to gravitationally grow. When this happens, radiation starts to stream out of this overdense region, suppressing its growth a little bit. As the radiation streams outward, however, it acts differently on the normal matter than on the dark matter.
- Because radiation collides with and scatters off of charged particles, it can push the normal matter outward; the normal matter attempted to gravitationally collapse, but the outward-streaming radiation then pushes this normal matter back out, causing it to “bounce” or “oscillate” rather than just collapse.
- Because radiation doesn’t collide with or scatter off of dark matter, however, it doesn’t receive the same push outward. The radiation can still stream outward, but other than gravitationally, there’s no effect on dark matter.

Think about what this means. If the Universe’s matter were composed 100% of normal matter and 0% of dark matter, we would see these enormous bouncing, oscillatory effects. This would actually be one of the dominant effects for how matter gravitated, clumped, and clustered: driven by this phenomenon known as baryon acoustic oscillations. If the Universe’s matter were composed 0% of normal matter and 100% dark matter, these bouncing, oscillatory effects wouldn’t be present at all; things would gravitationally grow without any coupling between the radiation and the normal matter.
One of the strongest tests for “how much normal matter vs. how much dark matter” is present in the Universe is, then, to look at the radiation from precisely 380,000 years after the Big Bang: at the leftover bath of radiation known as the cosmic microwave background.
On very small cosmic scales, the normal matter will have oscillated many times over, and these density fluctuations will be damped away. On larger scales, there are fewer oscillations, and you’ll see “peaks” and “valleys” where you have constructive and destructive interference, respectively. And on one very specific cosmic scale — called “the acoustic scale” by astrophysicists — you’re seeing the normal matter where it peaks: where it gravitates and falls in, but where neutral atoms formed right at the moment that radiation would’ve otherwise begun to push it back outward.

This pattern, of “peaks and valleys” in the leftover glow from the Big Bang, teaches us an enormous amount of information about the Universe we inhabit. It teaches us that both normal matter and dark matter must be present, and must be present in about a 1:5 ratio, respectively. It also allows us to read off, by measuring the scale at which the maximum “peak” of fluctuations occurs, where the greatest-magnitude “bounce” should be occurring: on angular scales that take up about one degree on the sky. Or, at least, that took up about “one degree” on the sky, for whatever length scale that corresponds to when the Universe was only 380,000 years old.
That scale — the acoustic scale — then gets frozen-in to the Universe’s memory once neutral atoms form, because there’s no further interaction between the leftover radiation from the Big Bang and the normal matter. (Normal matter is transparent to this now long-wavelength, infrared radiation by the time the Universe is 380,000 years old.)
However, these overdense-and-underdense imprints will continue to evolve. They expand, in scale and size, as the Universe expands. While the overdense regions will continue to gravitationally grow and eventually form stars, galaxies, and even grander structures, the underdense regions will give up their matter to their denser surroundings, leading to the creation of cosmic voids.
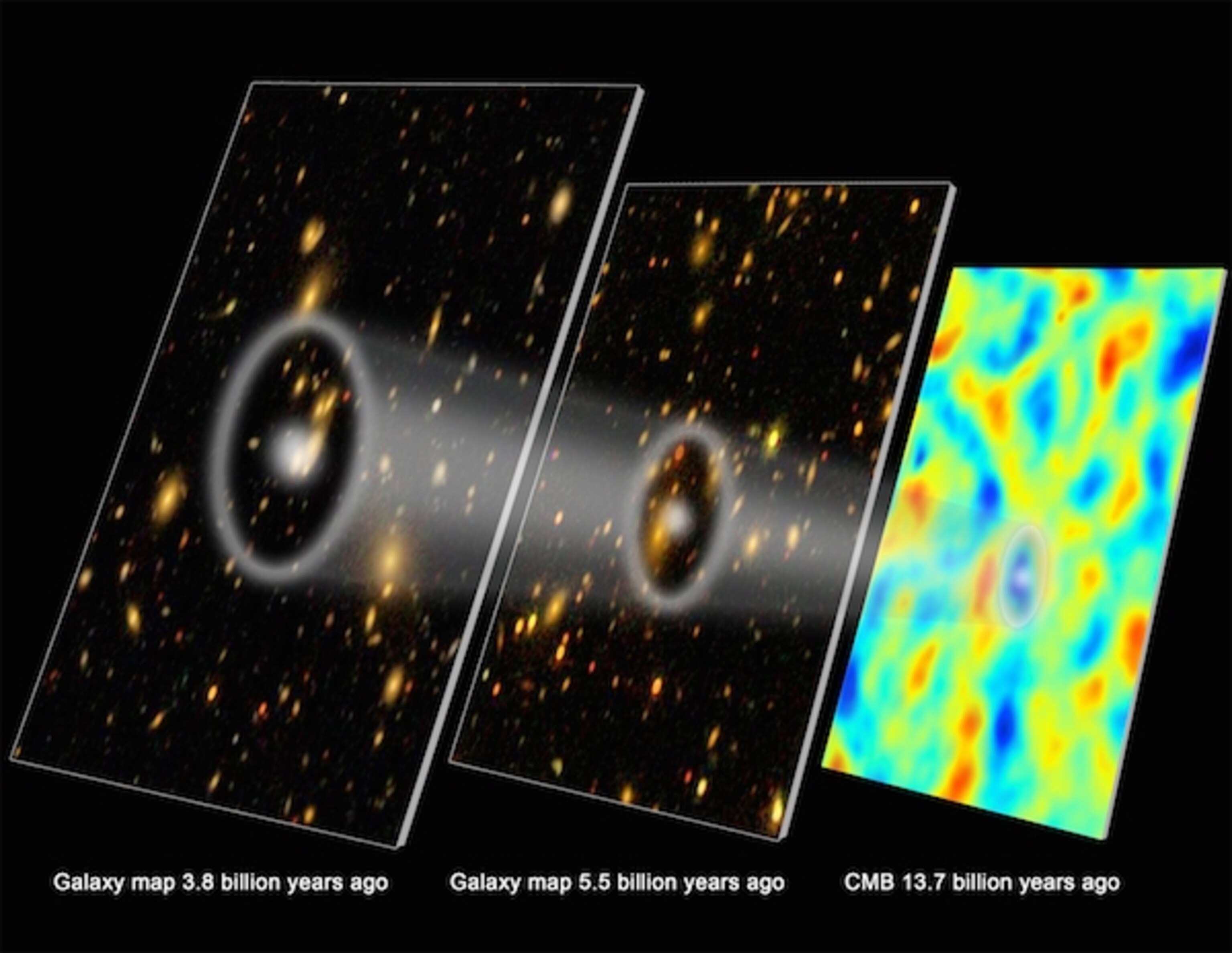
In other words, this signal of baryon acoustic oscillations shouldn’t just be imprinted in the cosmic microwave background (which it is), but also in the large-scale structure of the Universe. These oscillations exist on all scales, but the largest-magnitude, strongest oscillation should be on a scale that today, 13.8 billion years after the Big Bang, has grown to be approximately 500 million light-years across.
One of the places this will show up, in large-scale structure surveys of the Universe, is in something that astrophysicists call the “two-point correlation function.” Before you throw up your hands and say, “How am I ever going to understand something that complicated?” let me break it down in simple terms for you.
Imagine that you have a galaxy whose location you’ve measured in space. The two-point correlation function simply asks, “How likely am I to find another galaxy a certain distance away from this particular galaxy?” (At least, compared to complete randomness.) If there were no baryon acoustic oscillations at all, the answer would look like a smooth function: there would be a slowly-but-steadily decreasing likelihood of finding another galaxy at that precise distance the farther away you went. But if these baryon acoustic oscillations are present, it means that there’s a particular distance scale — the modern-day version of the ancient “acoustic scale” imprinted in the cosmic microwave background — that you’ll suddenly be more likely to find another galaxy, while slightly greater and smaller distances will show that you’re less likely to find such a galaxy.
Statistically, this has been borne out very robustly in the data. We’ve even been able to use large-scale structure surveys that go out into the distant Universe to measure how the acoustic scale has changed with time; improving this measurement is one of the major science goals that each of the Euclid, Roman, and Rubin Observatories have for themselves. The acoustic scale acts like a very special type of cosmic ruler, enabling us how this acoustic scale has expanded over cosmic time.
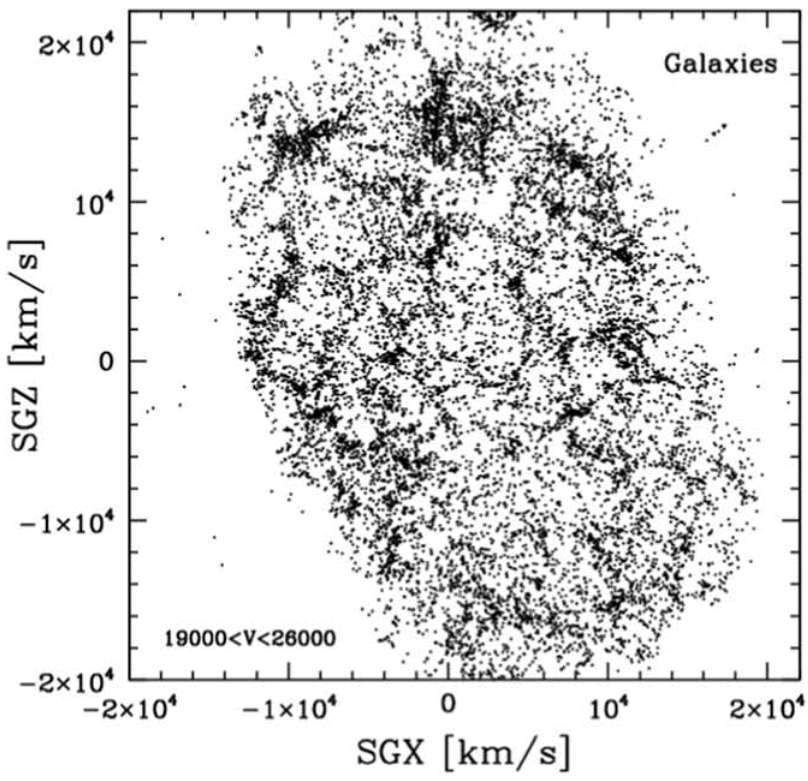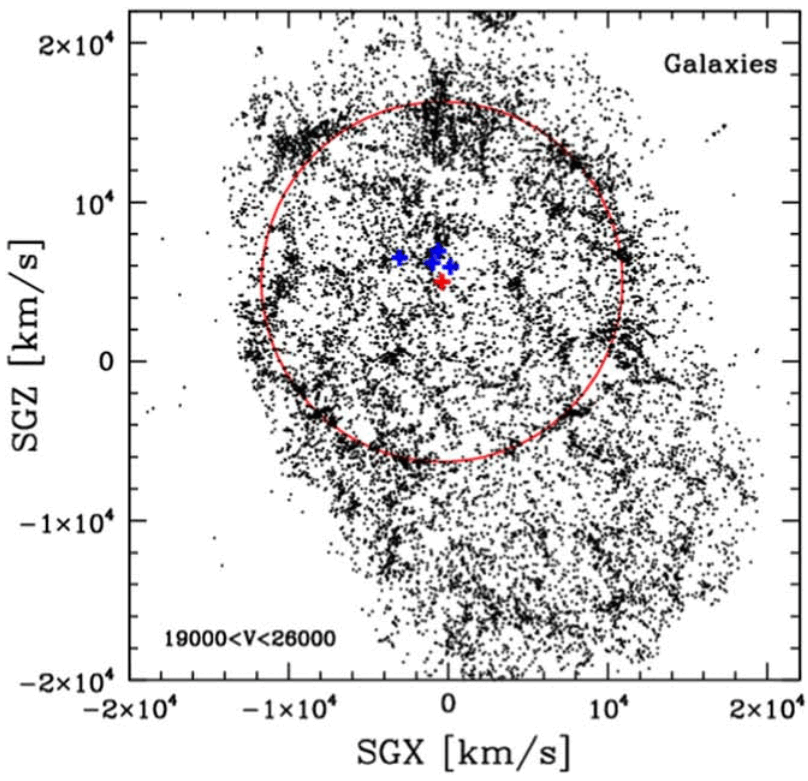
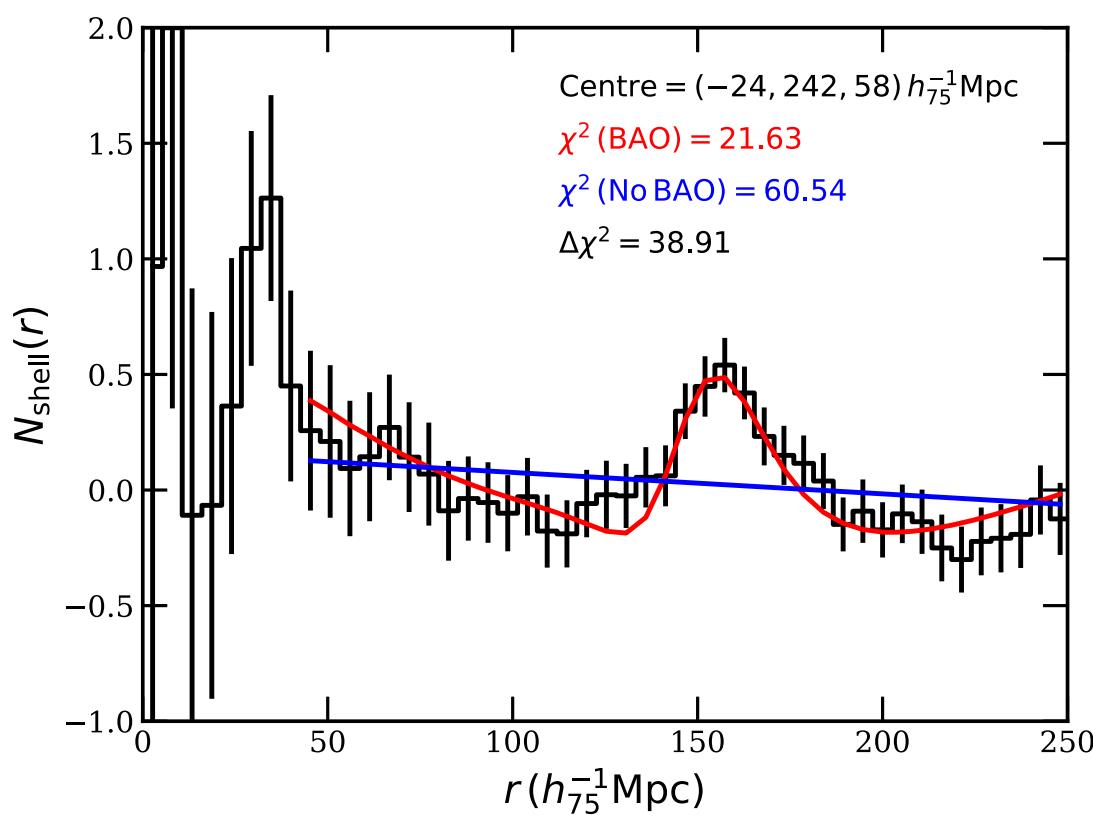
But in this new tour-de-force paper, Tully and his collaborators find evidence for an individual baryon acoustic oscillation for the first time: located around 820 million light-years away and spanning, just as you might expect, 500 million light-years in size. Sure enough, if you put down your finger on any galaxy and ask, “how likely am I, compared to just random chance, to find another galaxy a certain distance away from this one,” you’ll find that there’s a clear acoustic peak in the data for this one small volume of space: where you’re more likely to find a galaxy 500 million light-years away than either 400 or 600 million light-years away from another. The data is so strong that, already, it’s surpassed what’s considered the “gold standard” of 5-sigma statistical significance in just this first analysis.
The individual acoustic oscillation contains both clusters and voids within it, but it’s truly the overall structure and properties that matter, not the substructure within it. The authors gave this oscillation the name “Ho’oleilana,” which is a name that appears in the Hawaiian creation chant: Kumulipo, recounting the origin of structure in the Universe. Many structures familiar to both professional astronomers and astronomy enthusiasts are present within it, including:
- the Boötes Void,
- the Coma Great Wall,
- the edge of the Coma cluster of galaxies,
- and the Sloan Great Wall of galaxies.
Although the phenomenon of baryon acoustic oscillations has been well-known and even well-measured for a few decades now, it was very unexpected that current survey technology would actually be able to reveal a single, individual baryon acoustic oscillation. It’s even more surprising to many that the acoustic feature itself is even discernible from a simple visual inspection; you can practically see it for yourself in the raw data! While this will need to be further scrutinized to ensure that we aren’t fooling ourselves with this object, this is a tremendous victory for the consensus model of cosmology. Without dark matter, normal matter, and an expanding Universe containing them all, these features simply couldn’t be present. When it comes to an observational science like astronomy, seeing really is believing.
This article was reprinted with permission of Big Think, where it was originally published.





