Here in our Universe, whenever you gather enough mass together in a small enough volume of space, you’re bound to eventually cross a threshold: where the speed at which you’d need to travel to escape the gravitational pull within that region exceeds the speed of light. Whenever that occurs, it’s inevitable that you’ll form an event horizon around that region, which looks, acts, and behaves exactly like a black hole as seen from the outside. Meanwhile, inside, all that matter gets inexorably drawn toward the central region inside that black hole. With finite amounts of mass compressed to an infinitesimal volume, the existence of a singularity is all but assured.
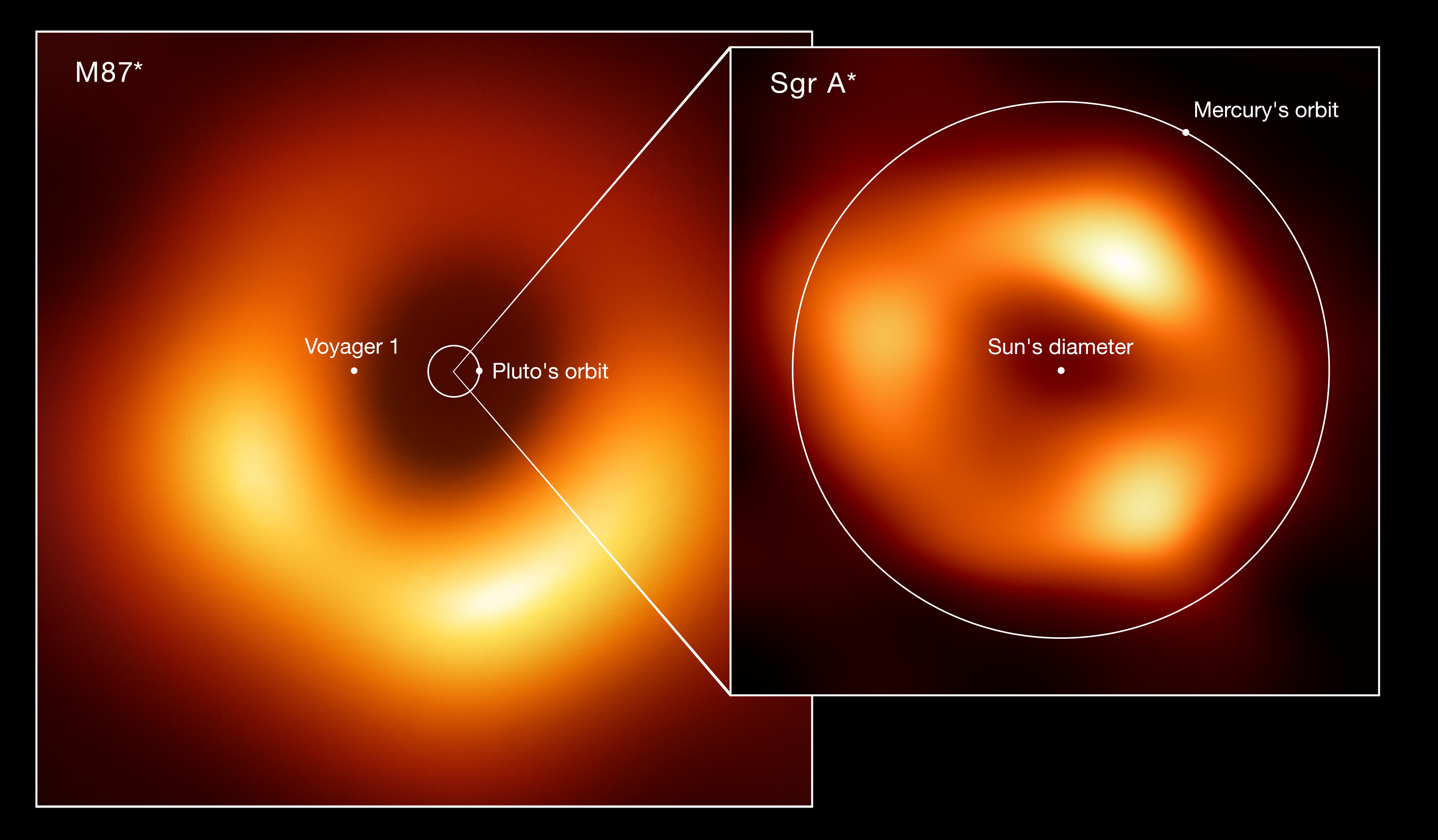
The predictions for what we should observe outside the event horizon match extraordinarily well with observations, as we’ve not only seen many luminous objects in orbit around black holes, but have even now imaged the event horizons of multiple black holes directly. The theorist who laid the foundation for how realistic black holes form in the Universe, Roger Penrose, subsequently won the Nobel Prize in Physics in 2020 for his contributions to physics, including for the notion that a singularity must exist at the center of every black hole.
But in a surprising twist, the legendary physicist who discovered the spacetime solution for rotating black holes — Roy Kerr, way back in 1963 — has just written a new paper challenging that idea with some very compelling arguments. Here’s why, perhaps, singularities may not exist within every black hole, and what the key issues are that we should all be thinking about.

Making an ideal black hole
If you want to make a black hole, in Einstein’s general relativity, all you have to do is take any distribution of pressureless mass — what relativists call “dust” — that starts in the same vicinity and is initially at rest, and let it gravitate. Over time, it will contract down and down and down to smaller volumes, until an event horizon forms at a specific distance from the center: dependent solely on the total amount of mass that you began with. This produces the simplest type of black hole known: a Schwarzschild black hole, which has mass, but no electric charge or angular momentum.
Einstein first put forth general relativity, in its final form, in late 1915. Just two months later, in early 1916, Karl Schwarzschild had worked out the mathematical solution for a spacetime that corresponds to this situation: a spacetime that’s completely empty except for one point-like mass. In reality, the matter in our Universe isn’t pressureless dust, but rather is made of atoms and subatomic particles. Nevertheless, through realistic processes like:
- the core-collapse of massive stars,
- the mergers of two massive-enough neutron stars,
- or the direct collapse of a large amount of matter, either stellar or gaseous,
black holes certainly form in our Universe. We’ve observed them, and we’re certain they exist. However, a big mystery remains: what happens inside of them, in their interiors, where we cannot observe?
The argument for a singularity
There’s a simple argument you can make to understand why we think that all black holes, at least under the Schwarzschild set of assumptions, ought to have a singularity at their centers. Imagine you’ve crossed over the event horizon, and are now on the “inside” of the black hole. Where can you go from here?
- If you fire your thrusters directly at the singularity, you’ll just get there faster, so that’s no good.
- If you fire your thrusters perpendicular to the direction of the singularity, you’ll still get drawn inward, and there’s no way to get farther from the singularity.
- And if you fire your thrusters directly away from the singularity, you’ll find that you’re still approaching the singularity faster and faster as time goes on.
The reason why? Because space itself is flowing: like a waterfall or a moving walkway beneath your feet. Even if you speed yourself up so that you’re moving arbitrarily close to the speed of light, the rate at which space is flowing is so great that no matter which direction you move in, the singularity appears to be “down” in all directions. You can draw out the shape of where you’re allowed to go, and even though it forms a mathematically interesting structure known as a cardioid, all paths lead to you winding up at the center of this object. Given enough time, these black holes should all have a singularity at their centers.

The Kerr advance: adding rotation
But here in the real Universe, the ideal case of having a mass with no rotation to it isn’t exactly a good physical model of reality. Consider that:
- there are many masses in the Universe,
- these masses, over time, gravitationally attract one another,
- causing them to move relative to one another,
- which leads to the clumping and clustering of matter in a non-uniform way,
- and that as clumps of matter move relative to one another and gravitationally interact, they’ll exert not just forces but torques on one another,
- that torques cause rotation,
- and that as rotating objects collapse, their rotation rate increases due to the conservation of angular momentum,
it makes sense that all physically realistic black holes would be rotating.
It turns out that while asking the question of what does a spacetime look like if you have only a single point mass in your Universe is a relatively straightforward problem to solve in Einstein’s general relativity — after all, Karl Schwarzschild solved it in just a couple of months — the question of what spacetime looks like if you have a mass that rotates is much more complicated. Indeed, many brilliant physicists worked on this problem and were unable to solve it: for months, years, and even decades.
But then, in 1963, New Zealand physicist Roy Kerr finally cracked it. His solution for the spacetime describing realistic, rotating black holes — the Kerr metric — has been the gold standard for what relativists have used to describe it ever since.
Rotation and reality
When you add rotation in, the situation for how spacetime behaves suddenly becomes a lot more complicated than it was in the non-rotating case. Instead of a spherical event horizon marking the delineation between where it’s possible to escape the black hole (outside) versus where escape is impossible (inside), and instead of all “inside” paths leading to a singularity at the center, the mathematical structure of a rotating (Kerr) black hole looks extremely different.
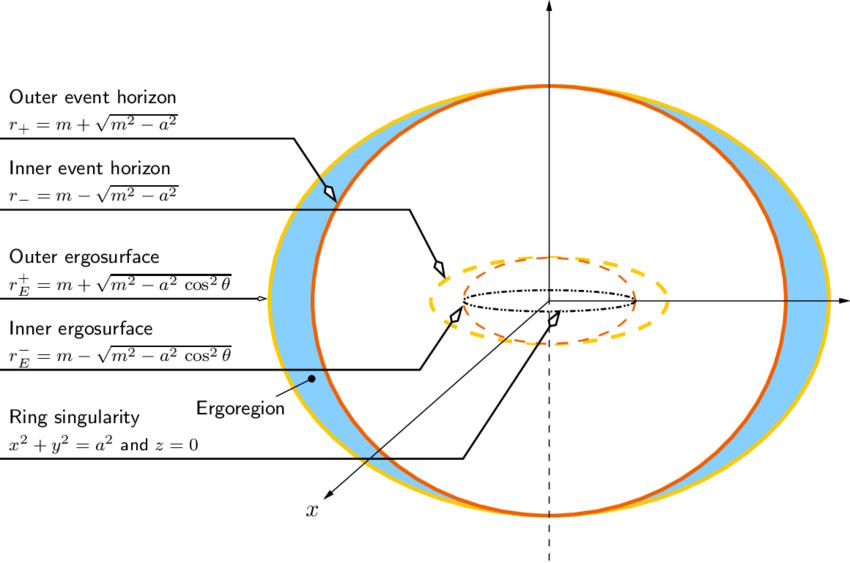
Instead of a single, spherical surface describing the event horizon and a point-like singularity at the center, the addition of rotation causes there to be several important phenomena that aren’t apparent in the non-rotating case.
- Instead of a single solution for the location of the event horizon, as in the Schwarzschild case, the equation you wind up with in the Kerr case is quadratic, giving two separate solutions: an “outer” and “inner” event horizon.
- Instead of the event horizon marking the location where the timelike component of the metric flips sign, there are now two surfaces that are different from the inner and outer event horizons — the inner and outer ergospheres — that delineate those locations throughout space.
- And instead of a zero-dimensional, point-like singularity at the center, the angular momentum present smooths that singularity into a one-dimensional surface: a ring, with the rotational axis of the black hole passing perpendicular through the center of the ring.

This leads to a variety of, shall we say, less-than-intuitive effects that occur within a Kerr spacetime that don’t occur within a Schwarzschild (non-rotating) spacetime.
Because the metric itself has an intrinsic rotation to it and couples to all of space outside the event horizons and ergospheres, all outside inertial reference frames will experience an induced rotation: a frame-dragging effect. This is similar to electromagnetic induction, but for gravitation.
Because of the non-spherically symmetric nature of the system, where we now have one of our three spatial dimensions representing a rotational axis and where there’s a direction (clockwise or counterclockwise, for example) to that rotation, a particle that orbits this black hole won’t make a closed ellipse that remains in the same plane (or a slowly-decaying and precessing ellipse, if you account for all of general relativity’s effects), but rather will move throughout all three dimensions, eventually filling in a volume enclosed by a torus.
And, perhaps most importantly, if you track the evolution of any particle that falls into this object from outside, it won’t simply cross over to the inside of the horizon and head inexorably toward the central singularity. Instead, other important effects occur that may work to “freeze” these particles in place, or to otherwise prevent them from traveling all the way to the theoretical “ring” singularity at the center. That’s where we owe it to ourselves to take a good look at what Roy Kerr, who’s been thinking about this puzzle for longer than anyone else alive, has to say about it.
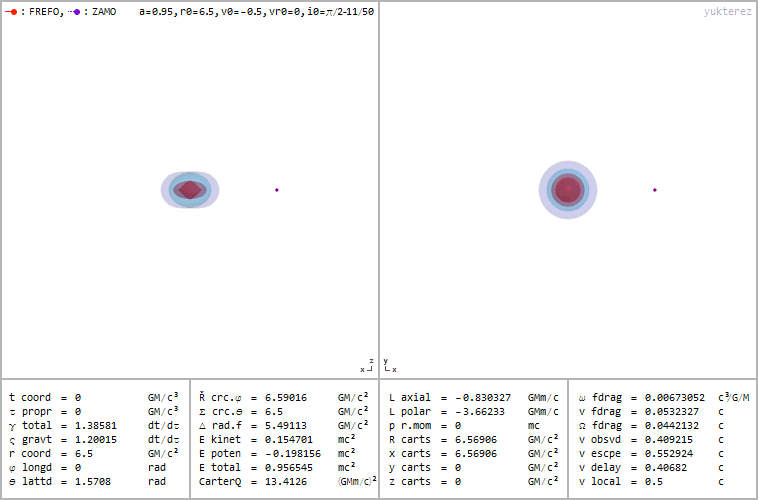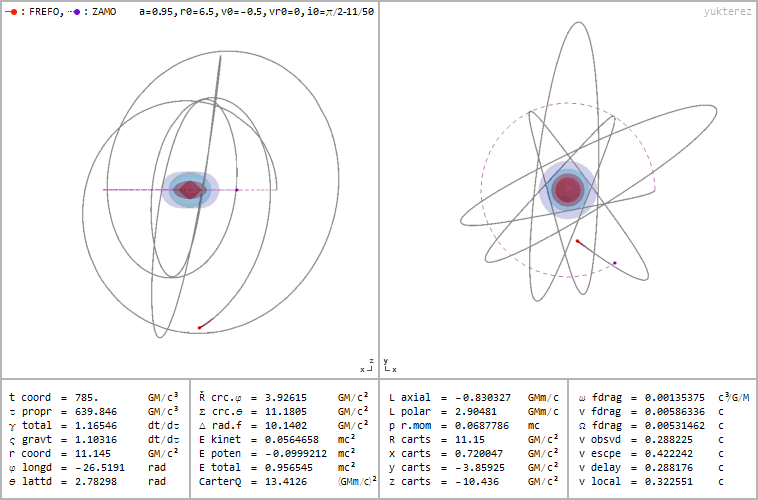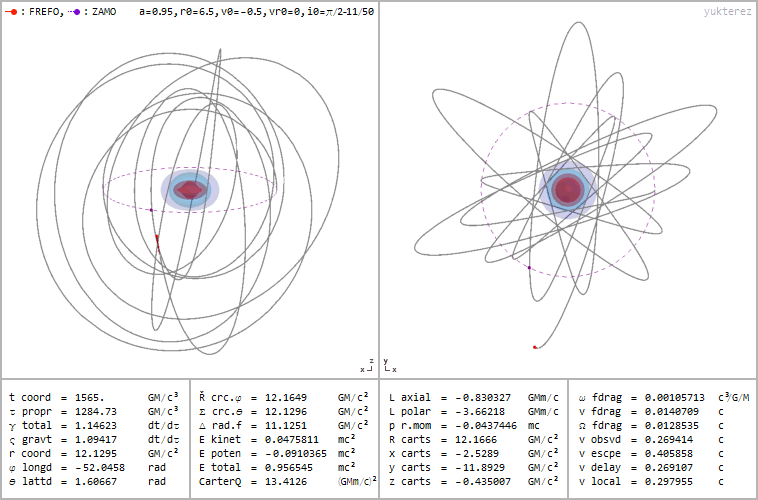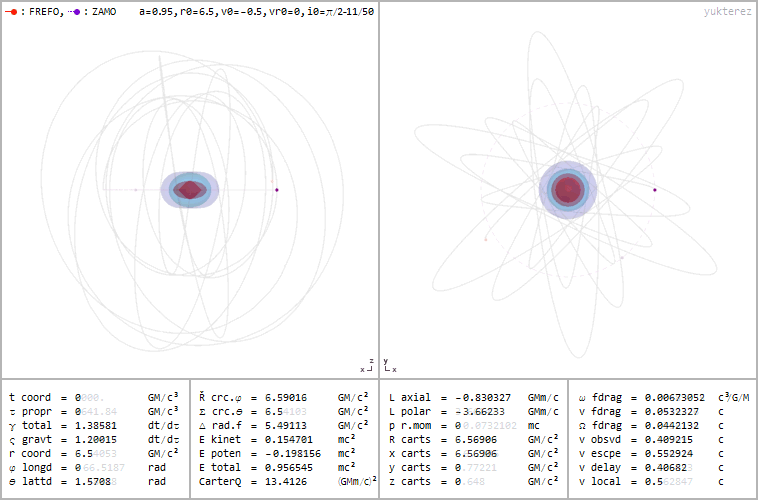
Revisiting the argument for a singularity
The biggest argument for why a singularity must exist inside of black holes comes from two titanic figures in 20th century physics: Roger Penrose and Stephen Hawking.
- The first part of the argument, from Penrose alone, is that wherever you have what’s called a trapped surface — a boundary from which nothing physical can escape, e.g., an event horizon — any light rays interior to that trapped surface will possess a mathematical property known as having finite affine length.
- This “finite affine length light,” or FALL, for each light ray then implies that the light must terminate in an actual singularity, which is the second part of the argument from Penrose and Hawking.
- You can then show that any object that enters the region between the outer and inner event horizons must “fall through” to the interior.
- And, because you need a source to generate the spacetime, the existence of a ring singularity is required.
At least, that’s how the traditional argument goes. The third and fourth parts of the argument are airtight in general relativity: if parts one and two are true, then you need a singularity at the core. But are parts one and two both true? That’s where Kerr’s new paper comes into play, asserting that no, this is a mistake that we’ve been making for over half-a-century.

What Kerr showed is that if you go all the way back to his original, generalized coordinate formulation for Kerr black holes, the Kerr-Schild coordinates, through every single point in the interior of the Kerr black hole, you can draw light rays that are:
- tangential (i.e., approach but do not intersect) to one of the two event horizons,
- do not have endpoints (i.e., they continue to travel forever),
- and yet still have finite affine lengths (i.e., they are FALLs).
Moreover, if you ask the key question, “How common are these light rays?” the answer is that there are an infinite number of them, and that half of these rays are in the region between the two event horizons, with at least two through every point in that region.
The problem, as Kerr has been able to show, is with point #2 in the aforementioned argument. Sure, you have a trapped surface in Kerr spacetime, and all the light rays within that trapped surface have finite affine length. But is that light required to terminate in a singularity? Not at all. In fact, by demonstrating the presence of these light rays that are tangential to an event horizon and that do not have endpoints, he has provided a counterexample to that notion. In Kerr’s own words:
“It has not been proved that a singularity, not just a FALL, is inevitable when an event horizon forms around a collapsing star.”
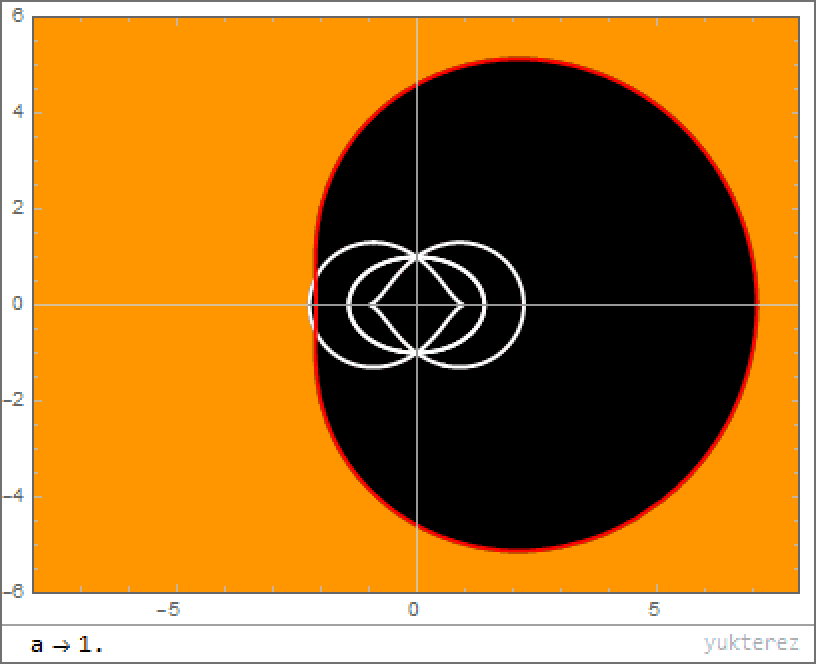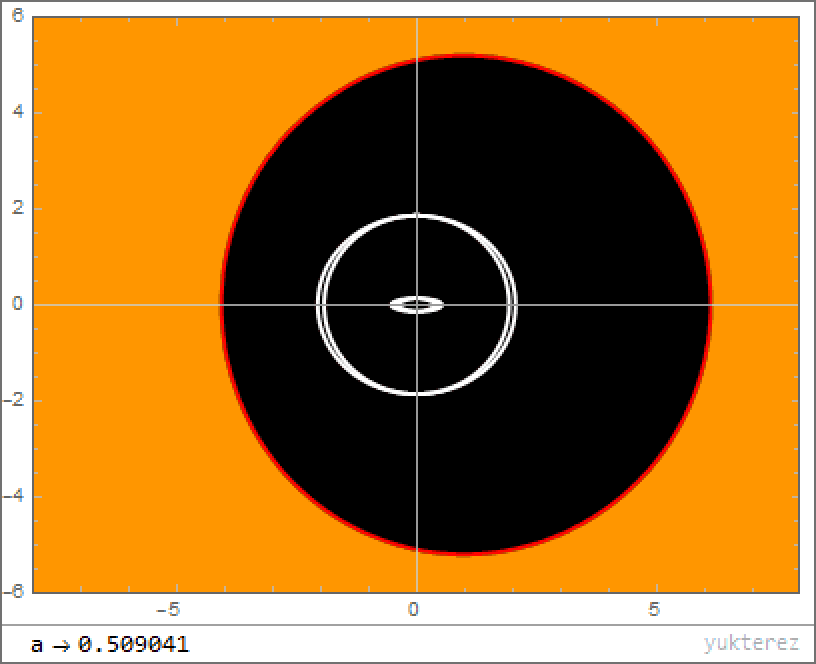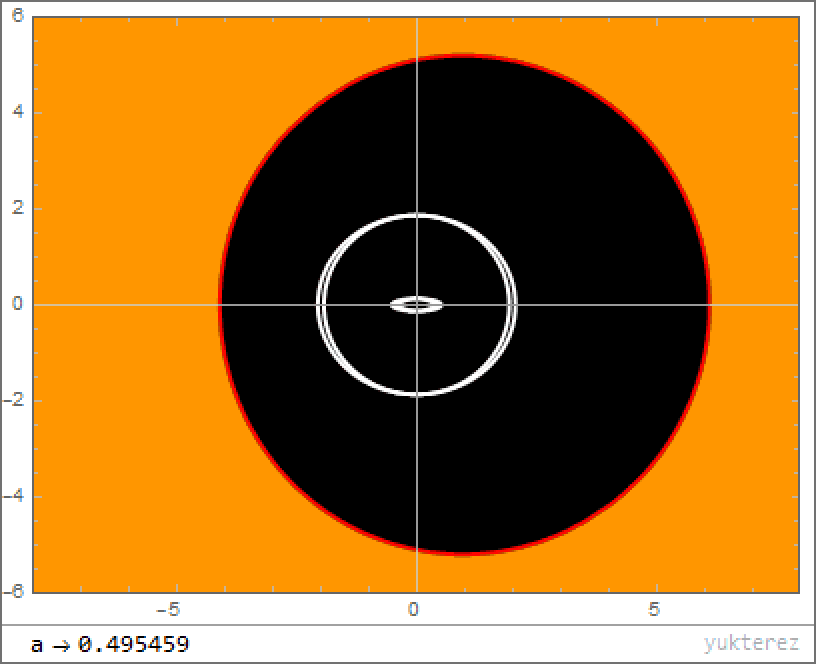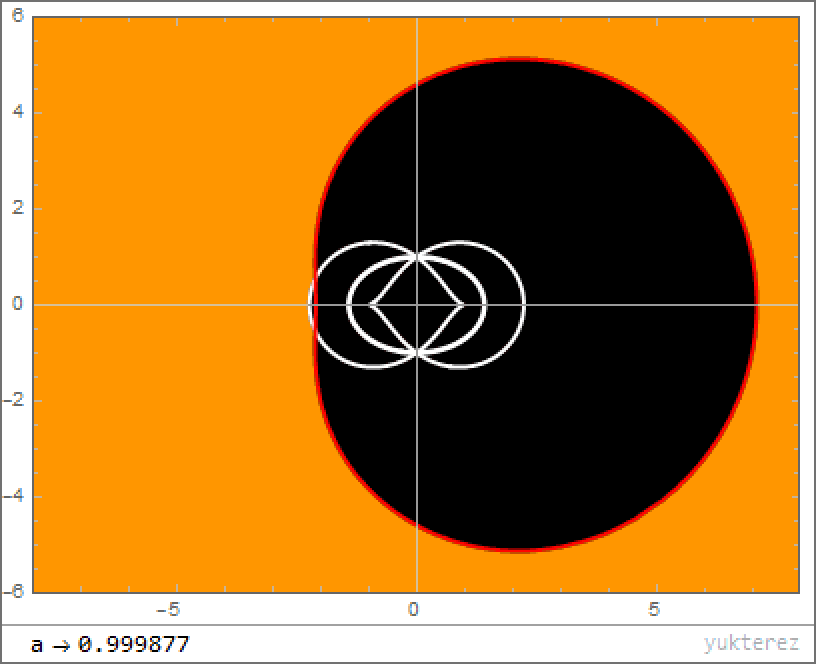
The problem with Hawking & Penrose
It’s kind of remarkable, if you go back in history, to realize how much of our acceptance of the existence of a singularity depends on an unproven assertion. Back in 1970, Hawking and Penrose wrote a paper called The singularities of gravitational collapse and cosmology, and within it note that there are other possibilities to consider than the traditional (curvature) singularities when it comes to realistic black holes.
With the disproof that Kerr has demonstrated, some people have instead asserted that you need to consider the maximal extensions of the Kerr space, and you’ll find the need for a singularity there. For example, in the Boyer-Lindquist extension of the Kerr spacetime, you have a collection of copies of the separate parts of the original Kerr metric, and because there are no interior collapsed stars inside, it’s certain to be singular.
But again, as Kerr points out, you must assume that each interior section of the spacetime, even in the Boyer-Lindquist extension, contains a (collapsed) star within it, and therefore encounters the same problem. Other extensions (such as Kruskal) have been proposed, but Kerr shot those attempts to evade this problem down as well, by demonstrating that Kerr is its own maximal extension. As Kerr puts it:
“These extensions may be analytic, but at best they are constructed using copies of the original spaces together with some fixed points. These will be nonsingular inside each copy of the original interior if the same is true inside the original Kerr and therefore the extensions are irrelevant to the singularity theorems. Anyone who does not believe this needs to supply a proof. They are all physically irrelevant since real black holes start at a finite time in the past with the collapse of a star or similar over-dense concentration of matter, not as the white hole of the Kruskal or Boyer-Lindquist extensions.”
Put simply: a FALL does not necessarily mean a singularity, and Kerr chalks the confusion up to physicists conflating geodesic distance/length with affine distance/length: two concepts that are not, in fact, identical. Kerr also points out that if there were a nonsingular object, like a stretched-out neutron star corpse, inside the Kerr black hole, it too would generate the Kerr spacetime we observe. In other words, there are good reasons to revisit the notion that a singularity must exist inside each realistic, rotating black hole.

Final thoughts
We have to remember an important aspect of general relativity that almost everyone — laypersons and physicists alike — often overlook: “general relativity is about forces, not geometry.” The person who said that wasn’t some crackpot; it was Einstein himself. general relativity is not simply pure mathematics; it’s a description of the physical Universe, placed on a firm mathematical footing. You can’t simply “write down a spacetime” and expect that to describe reality, you have to start from a physically motivated set of conditions and show how that spacetime solution (e.g., a rotating black hole) comes to be. If the only way you can “prove” the existence of a singularity is by ignoring the physical creation of the object in the first place, your proof is not valid.
However, demonstrating a counterexample to your attempted proof, both physically and mathematically, is an excellent way to falsify any assertion that gets made. With Kerr’s latest work — a full 60 years after first deriving the Kerr metric — we have to reckon with the sober fact that our best “singularity theorems” that argue for their necessity at a realistic black hole’s center are based on an invalid assumption.
Furthermore, once you cross over to be inside the inner event horizon in Kerr spacetime, it once again becomes possible to travel in any direction between the theorized ring singularity and the inner event horizon. The “trapped surface” only exists between the inner and outer event horizons, not interior to the inner event horizon: where the ring singularity allegedly exists. Who knows what exists in that region? The problem is that there are enormous numbers of mathematical solutions to this problem, and “a singularity” is only one of them. There might indeed yet be a singularity inside, but there also may be something entirely different. Kerr, currently at the age of 89, has no problem telling us what he thinks, writing that he:
“has no doubt, and never did, that when relativity and quantum mechanics are melded it will be shown that there are no singularities anywhere. When theory predicts singularities, the theory is wrong!”
What we can be certain of is that the long-accepted “proof,” that rotating black holes must have singularities, can’t be counted on any longer. (You can download and read Kerr’s latest paper for free here.)
This article was reprinted with permission of Big Think, where it was originally published.





