The world forever changed back in February of 2016, when the LIGO collaboration made a revolutionary announcement that altered our view of the Universe forever. From more than a billion light-years away, two massive black holes, of 36 and 29 solar masses, had inspiraled and merged. The result of that merger was a single black hole of 62 solar masses, with the remaining 3 solar masses converted into pure energy via Einstein’s E = mc², rippling throughout the Universe in the form of gravitational waves. At last, no one could doubt the physical reality of gravitational waves, including the facts of:
- how they were produced,
- that they unambiguously carried energy throughout the Universe,
- and that they traveled at their theoretically predicted speed of c, the speed of light in a vacuum.
Since that time, LIGO has been joined by additional gravitational wave detectors such as Virgo, has risen into the triple-digits as far as the number of detections it’s made, and has witnessed neutron star mergers as well as black hole mergers, spanning nearly a factor of ~100 in the mass ranges of their detected objects. Gravitational waves are now undoubtedly real, and the process of observing them is teaching us an incredible amount about our Universe. But all of this information still only probes the predictions that arise from our classical theory of gravity: general relativity.
If quantum physics is right, then wave-particle duality must be real, even for gravitational waves. Here’s what that means, and how we might someday go about putting it to the ultimate, experimental test.

It’s no stretch to claim that wave-particle duality is one of the strangest quantum phenomena ever uncovered. The independent ideas of waves and particles started out simply enough: matter was made of particles, things like atoms and their constituents, and radiation was made of waves. You could tell something was a particle because those things would exhibit behaviors like colliding and bouncing off of other particles, sometimes they would stick together and create composite particles, often colliding particles would exchange energy and momentum, occasionally they can create bound states that lead to the emission of other particles, and so on.
Similarly, you could tell if something was a wave because it would exhibit wave-like phenomena, such as diffraction and interference, both with other waves and also with itself. Newton got this one wrong about light, thinking it was made of particles, but others such as Huygens (his contemporary) and then the early-1800s scientists like Young, Fresnel, and Arago showed definitively that light exhibited properties that couldn’t be explained without considering it as a wave.
Perhaps the most obvious wave-like phenomenon of all, interference, appears when you pass light through a double slit. The pattern that shows up on a background screen shows that the light interferes both constructively (leading to bright spots) and destructively (leading to dark spots).
This phenomenon, of interference, is uniquely a product of wave-like behavior. The double slit experiment, and subsequent, more sophisticated analogues, established that light was a wave. By the end of the 19th century, it was pretty clear that some things exhibited wave-like properties, like light, sound, and fluids, while others exhibited particle-like properties.
The distinction between those two types of behavior got more confusing in the early 1900s, however, with the discovery of the photoelectric effect. When you shone light on a certain material, occasionally electrons would get “kicked off” by the light.
The details of how the photoelectric effect worked, however, showed that it wasn’t the cumulative energy (or intensity) of the light that kicked electrons off, but rather the specific wavelength (or energy) components of that light that were responsible. If you made the light that was causing these electrons to be “kicked off” redder than a specific threshold (and hence, lower in energy) — even if you made the light arbitrarily intense — the light wouldn’t kick off any electrons. But if you kept the light that was bluer than that same specific “ionization” threshold (i.e., higher energy light), even if you turned the intensity way, way down, you’d still kick off electrons. Shortly thereafter, we were able to discover that light is quantized into photons, and that even individual photons could act like particles, ionizing the electrons if they were of the right energy.

Even stranger realizations came in the 20th century, as we discovered that:
- Single photons, when you passed them through a double slit one-at-a-time, would still interfere with themselves, producing a pattern consistent with a wave nature.
- Electrons, known to be particles, exhibited this interference and diffraction pattern as well.
- Composite particles, and even tiny living organisms, can interfere with themselves as you pass them through a double slit.
- However, if you measured which slit a photon or electron went through, you wouldn’t get an interference pattern, at all. You will only get one if you don’t make that measurement.
It seems that every particle we’ve ever observed can be described as both a wave and a particle. The big lesson from quantum physics isn’t that things are either “waves” or “particles” inherently, but rather it teaches us that we need to treat all objects as both-or-either a wave and/or a particle, dependent on the physical circumstances of the scenario under consideration. If we insist on treating a phenomenon as acting like a “wave” or a “particle” 100% of the time, we simply won’t get outcomes that agree with our experiments.
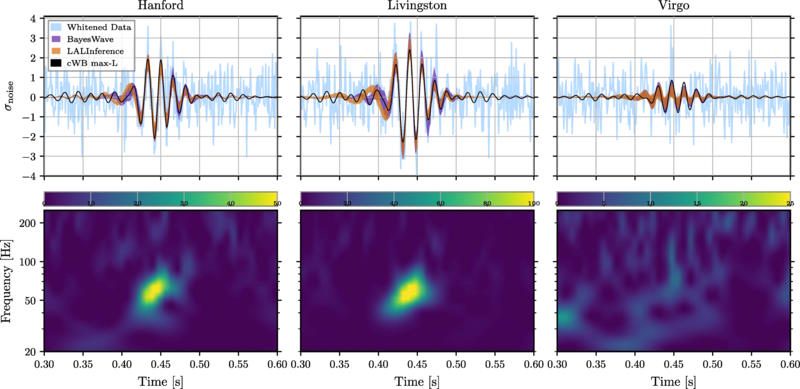
Now, at last, we’re ready to consider gravitational waves. These waves are sort of unique as far as physics is concerned, because we’ve only seen the wave-like part of them, never the particle-based part. This is because, even though we have often assumed that reality is quantum in nature, we’ve never been able to put gravitation to the test to determine whether it exhibits this inherently quantum behavior or not.
However, just like water waves are waves that are made of particles, we fully expect that gravitational waves are made of particles, too. When you see ripples in a pond, waves in an ocean, or the propagating splash from someone who jumps into a swimming pool, you’re clearly observing a wave-like phenomenon on a macroscopic scale. But microscopically, water is made up of individual molecules — enormous numbers of them — that all interact together. It’s only from their combined motions, all added up, that the wave-like behavior emerges.
For gravitation, the particles composing gravitational waves (as opposed to water waves) ought to be gravitons (instead of water molecules), the particle that mediates the force of gravity under all known ideas that can give you a quantum theory of gravity. Gravitons are fully expected to emerge as a consequence of gravity being an inherently quantum force in nature, and just as light is composed of photons, gravitational waves ought to be composed of gravitons.

Because it’s a wave, and because that wave has been observed to behave exactly as general relativity predicts, including:
- during the inspiral phase,
- during the merger phase, and
- during the ringdown phase,
we can safely infer that it will continue to do all the wave-like things that general relativity predicts. They’re a little different in detail than the other waves we’re used to: they’re not scalar waves like water waves, nor are they even vector waves like light, where you have in-phase, oscillating electric and magnetic fields.
Instead, these are tensor waves, which causes space to contract and rarify in mutually perpendicular directions as the wave passes through that area, as the following video illustrates.
These waves do a lot of the same things you’d expect from any sort of wave, including that
- they propagate at a specific speed through their medium (the speed of light, through the fabric of space itself),
- they interfere with any other ripples in space both constructively and destructively,
- these waves “ride” on top of whatever other spacetime curvature is already present,
- and if there were some way to cause these waves to diffract — perhaps by traveling around a strong gravitational source like a black hole — they would do exactly that.
In addition, as the Universe expands, we know these waves will do what all waves in the expanding Universe do: to stretch and expand as the background space of the Universe expands, too.
So the real question is, then, how do we test the “quantum” part of this idea? How do we look for the “particle-like” nature of a gravitational wave?
In theory, a gravitational wave is similar to the earlier image that shows an apparent wave arising from many particles that move around: those particles are the gravitons and the overall apparent wave is what LIGO detected. There’s every reason to expect we’ve got a series of gravitons on our hands, that are:
- spin-2 particles,
- that are massless,
- that propagate at the speed of light,
- and that only interact through the gravitational force.
The constraints from LIGO on the second property of gravitons — their masslessness — are extremely good: if the graviton does have a mass, it’s less than 1.6 x 10-22 eV/c², or some ~1028 times lighter than the electron. But until we figure out a way to test quantum gravity using gravitational waves, we won’t know whether the “particle” part of wave-particle duality holds for gravitons.
There are actually a few opportunities for such a test, although LIGO and other gravitational wave observatories are unlikely to perform any of them in their current incarnation. You see, quantum gravitational effects are strongest and most pronounced where you have strong gravitational fields in play at very tiny distances. What better tool could there possibly be to probe this regime than merging black holes?
When two singularities merge together, these quantum effects — which should be departures from general relativity — will show up at the moment of the merger, and just before (at the end of the inspiral phase) and just after (at the start of the ringdown phase) the merger occurs. Realistically, we’re looking at probing picosecond timescales rather than the micro-to-millisecond timescales LIGO is sensitive to, which would require an enormous advance in the time-domain sensitivity of gravitational wave experiments.
Is this a physical impossibility? Not necessarily. LIGO, remember, is driven by lasers that shine through vacuum cavities, bounce off of mirrors thousands of times, and then have their light reconstructed and brought back together. Now consider this fact: we’ve developed laser pulses that work in the femtosecond or even attosecond (10-15 s to 10-18 s) time ranges, and so it’s conceivable that we could be sensitive to tiny departures from relativity if we have enough of these interferometers going at once. It would take a tremendous leap in technology, including a large number of interferometers, and a significant reduction in noise and increase in sensitivity. But it’s not technically impossible; it’s just technologically difficult!

Although we have every reason to believe that gravitational waves are simply the quantum analog of electromagnetic waves, we have, unlike the electromagnetic photon, not yet risen to the technological challenges of directly detecting the gravitational particle that’s the counterpart of gravitational waves: the theoretical graviton. While current gravitational wave detectors don’t yet have the time-domain sensitivity to probe whatever quantum gravitational effects may arise right around either side of the exact moment of black hole-black hole mergers, it’s not a technological or theoretical impossibility: just a tremendous challenge.
Theorists are still calculating the uniquely quantum effects that should arise and are working together with experimentalists to design tabletop tests of quantum gravity, all while gravitational wave astronomers puzzle over how a future-generation detector might someday reveal the quantum nature of these waves. Although we expect gravitational waves to exhibit wave-particle duality, until we detect it, we cannot know for certain. Here’s hoping that our curiosity compels us to invest in it, that nature cooperates, and that we find out the answer once and for all!
This article was reprinted with permission of Big Think, where it was originally published.






